
3 years full-time; 6 years part-timeUndergraduate
BA (Hons)
English Literature & Film
If you are a big fan of the sort of books and films that have stood the test of time and how the two relate, then this course is made for you. In our English Literature and Film degree you consider the disciplinary differences of literature and film as well as their interdependence, as many films begin as screenplays and many novels have been adapted for the big screen.
3 years full-time
6 years part-timeUndergraduate
BSc (Hons)
Forensic Investigation
On our dynamic three-year programme you engage with the key issues surrounding forensic detection methods. Combining elements of criminology, psychology and archaeology you are introduced to a wide range of applied investigative techniques, grounded in both classic and contemporary theoretical perspectives.
3 years full-time; 6 years part-timeUndergraduate
BSc (Hons)
Forensic Investigative Psychology
Are you intrigued by the human mind? Are you keen to learn how psychologists can use scientific research methods to contribute to the investigative process of the police and the wider criminal justice system? Within our popular Forensic Investigative Psychology degree, you will explore topics such as eyewitness memory, mental disorder in crime, and juror decision making.-Music-and-Sound-Production_1-1.jpg)
3 years full-time; 6 years part-timeUndergraduate
BA (Hons)
Music and Sound Production
Does professional studio recording and sound design thrill you? Are you seeking to push audio boundaries, discover emerging musical trends or forge new collaborations with musicians and creative artists? You can achieve all this and more on our Music and Sound Production programme, which is designed to provide you with an in-depth exploration of music and sound’s role in the convergent media industries of today enabling you to become the professional you want to be.
3 years full-time; 6 years part-timeUndergraduate
BA (Hons)
Musical Theatre
Musical theatre dazzles, inspires and entertains us. But it’s not all about singalongs and dancing in the aisles, there is business behind the show. Musicals exist as cultural artifacts that have been used to divert us from the pressures of the world and to confront social issues head-on using humour, passion, and pathos.
3 years full-time; 6 years part-timeUndergraduate
BA (Hons)
Philosophy
Philosophy is arguably the oldest university subject and has the widest field, with philosophers asking fundamental and important questions about values, culture, science, religion and society. As such Philosophy sits at the heart of any university, engaging with and enriching other programmes. In fact, at Winchester, Philosophy has a special role pledged to pioneering values-driven education and asking big questions about human existence.
3 years full-time; 6 years part-timeUndergraduate
BA (Hons)
Popular Music: Production and Performance
Popular Music: Production & Performance provides you the opportunity to learn in industry-standard facilities and be taught by industry practitioners. The programme embraces a practical approach to learning with a balance of practical workshops and lectures, promoting different learning styles.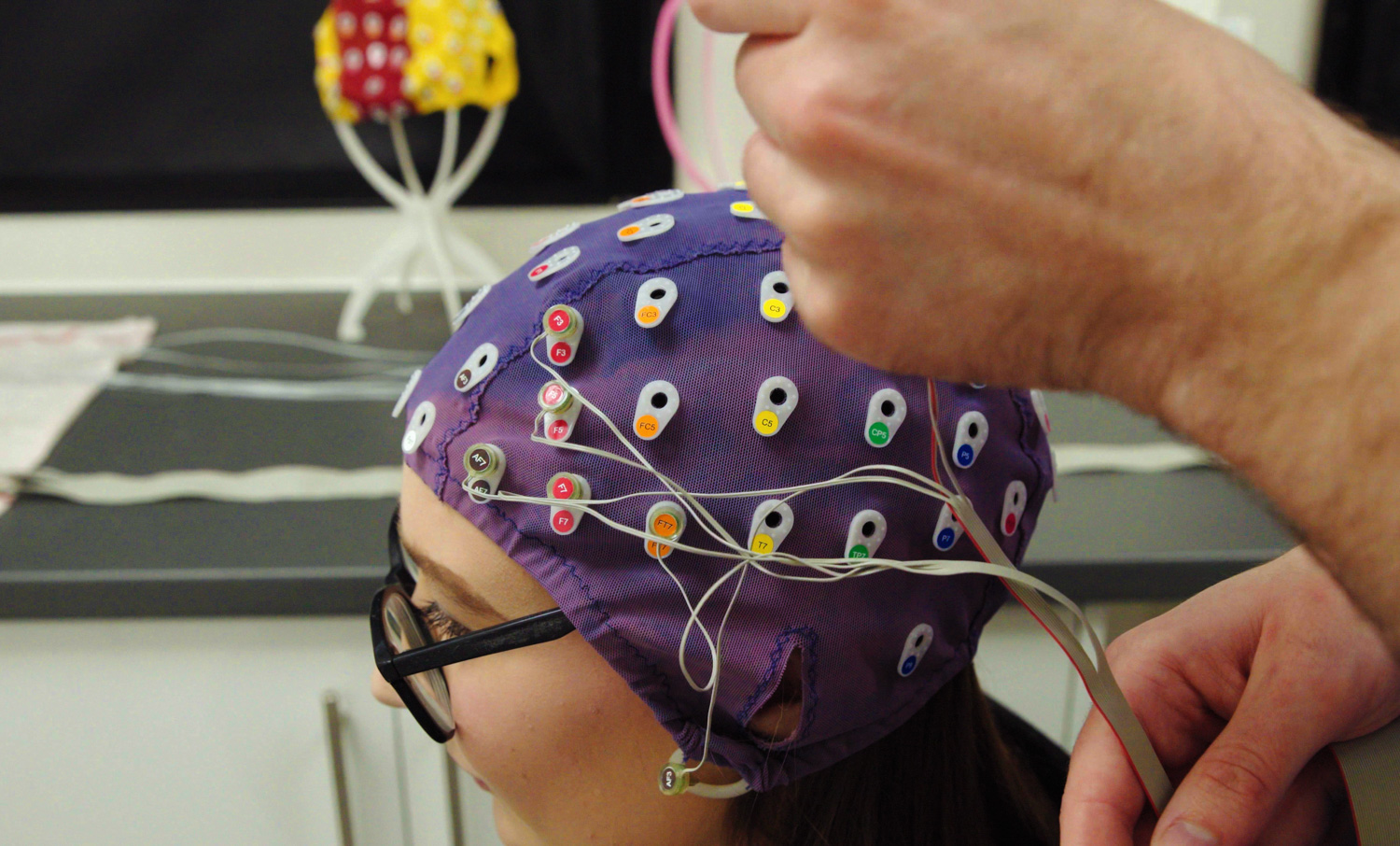
3 years full-time; 6 years part-timeUndergraduate
BSc (Hons)
Psychology
Curious about what drives behaviour? Fascinated by the human mind? Our Psychology degree will satisfy your interest as you discover the science behind how we think, feel and behave. You will join an active, supportive and inclusive community of students and staff and learn from experts passionate about their specialism who actively shape the discipline through their original research.
3 years full-time; 6 years part-timeUndergraduate
BSc (Hons)
Psychology and Child Development
Have a passion for working with children? Curious about how they learn and develop? Discover the fascinating science behind how children think, feel and behave. You will join an active, supportive and inclusive community of students and staff and learn from experts, passionate about their specialism. Our degree equips you with the knowledge and skills to study the mind and behaviour of children and prepares you for a fulfilling and meaningful career.
3 years full-time; 6 years part-time; 4 years sandwichUndergraduate
BSc (Hons)
